Метод рационализации при решении неравенств лекция по алгебре и началам анализа для 11 класса
Решение неравенств методом рационализации
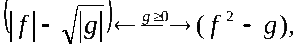
Автор Сергей Валерьевич
Воскресенье, Сентябрь 3, 2017
Данная статья посвящена разбору решенией неравенств (логарифмических и неравенств с модулем) методом рационализации.
Данный метод становится в последнее время всё более популярным, поскольку помогает существенно упростить решение неравенств, которые встречаются во второй части профильного ЕГЭ по математике.
Так что, если вы готовитесь к сдаче этого экзамена и не знакомы с решением неравенств методом рационализации, данная статья может оказаться для вас чрезвычайно полезной.
«Стандартный» метод решения логарифмических неравенств
Рассмотрим традиционный метод решения логарифмического неравенства на конкретном примере.
| Пример 1. Решить логарифмическое неравенство: |
Вне зависимости от того, каким методом вы решаете то или иное логарифмическое неравенство, начинать всегда нужно с области допустимых значений. Основание логарифма должно быть положительным и не равным 1, а выражение, стоящее под знаком логарифма, — положительным. То есть область допустимых значений в нашем примере определяется следующей системой:
Легко видеть, что решением данной системы является промежуток: .
Теперь, используя свойства логарифмов, представим двойку справа в виде логарифма с основанием . Тогда неравенства примет вид:
Далее решение неравенства разбивается на два случая:
1) если . В этом случае в основаниях логарифмов стоят одинаковые числа из интервала . Значит, соответствующие логарифмические функции являются убывающими. Поэтому, опуская знаки логарифмов, нам нужно изменить знак неравенства на обратный. В результате в этом случае приходим к следующему неравенству:
Изобразим соответствующую параболу, ветви которой направлены вверх, пересекающую ось OX в двух точках: и , являющихся корнями квадратного трёхчлена :Тогда с учётом рассматриваемого ограничения на получаем для этого случая .
2) рассмотрим теперь случай, когда . В этом случае оба логарифма будут возрастающими, поэтому после ухода от знаков логарифма, знак неравенства останется прежним. То есть в этом случае исходное логарифмическое неравенство можно заменить следующим:
В учётом ограничения на решение этого неравенства можно проиллюстрировать на числовой прямой следующим образом:
То есть решение в данном случае имеет вид: .
Объединяя решения, полученные в пунктах а) и б), приходим к окончательному ответу, который имеет вид: .
Решение логарифмических неравенств методом рационализации
Описанный в предыдущем параграфе способ является правильным, но при этом чрезвычайно неудобным. Как видите, приходится рассматривать два отдельных случая, что существенно повышает вероятность совершения ошибки. Гораздо проще поступить следующим образом. Перепишем исходное логарифмическое неравенства в виде:
А дальше, в области допустимых значений, то есть при (это мы установили выше), данное неравенство можно заменить следующим равносильным ему неравенством:
Ну действительно, если , то первая скобка положительна, и на неё можно разделить, не меняя при этом знак неравенства. Если же , то первая скобка отрицательна, и при делении на неё, знак неравенства изменится на противоположный.
То есть мы получили ровно то же самое, что имели в предыдущем пункте. Но при этом нет необходимости рассматривать два случая. Всё решается в рамках одного единственного неравенства. И хотя этот способ не избавляет нас от необходимости определения области допустимых значений, он всё равно приводит к существенному упрощению решения задачи.
Решаем полученное неравенство методом интервалов. Для этого поменяем знаки во второй скобке, разделим обе части неравенства на -1, поменяв знак неравенства:
Теперь разложим выражение во вторых скобках на множители:
Изобразим на числовой прямой множество решений полученного неравенства (стрелкой обозначена область допустимых значений исходного логарифмического неравенства):
В результате получаем тот же результат, что и в предыдущем параграфе:
.
Итак, метод рационализации логарифмических неравенств состоит в следующем.
в области его допустимых значений можно заменить равносильным неравенством
Здесь знак означает любой из знаков , , или .
С помощью этого метода можно решать и более сложные логарифмические неравенства. Рассмотрим ещё один пример из реальных прототипов заданий ЕГЭ по математике.
| Пример 2. Решите неравенство: |
Область допустимых значений данного неравенства определяется следующей системой неравенств:
Итак, область допустимых значений задаётся следующим промежутком:
.
Представим единицу справа в виде логарифма с основанием и перенесём его в левую сторону неравенства:
Воспользуемся методом рационализации. В области допустимых значений данное неравенство можно заменить следующим:
Умножим обе части на -4, поменяв при этом знак неравенства:
Разложим на множители выражение, стоящее в обеих скобках:
Если умножить обе части на 2 и внести этот множитель во вторую скобку, то получится следующее уравнение:
Изобразим на числовой прямой промежутки, на которые разбивают числовую ось корни полученного многочлена слева, определим знаки многочлена в каждом промежутке и выделим решение неравенства с учётом области допустимых значений:Итак, окончательный ответ:
.
Решение неравенств с модулем методом рационализации
Метод рационализации не ограничивается, конечно, возможностью решения лишь логарифмических неравенств. Вообще, суть метода в том, чтобы заменить «неудобные» части в выражении более простыми, которые имеют такой же знак, что и исходные части при тех же значениях . Поэтому метод рационализации применим к множеству различных неравенств. В том числе, к неравенствам с модулями.
К решению любого неравенства с модулем можно подойти стандартным образом. Раскрывать модули в зависимости от знаков подмодульных выражений при различных значениях . Однако, можно воспользоваться следующим свойством.
Знак выражения совпадает со знаком выражения при любых значениях . Это и используется при решении неравенств с модулями методом рационализации.
Неравенство типа
равносильно неравенству
Здесь знак означает любой из знаков , , или .
Ну действительно, известно, что и . Тогда обе части неравенства можно возвести в квадрат, перенести всё в одну сторону и воспользоваться формулой «разность квадратов»:
В этом и состоит суть метода рационализации неравенств, содержащих модули. Рассмотрим конкретный пример.
| Пример 3. Решите неравенство: |
Воспользуемся методом рационализации для решения данного неравенства. Заменим его равносильным и более простым неравенством:
Приведём подобные слагаемые в обеих скобках:
Из первой скобки вынесем множитель -10, а из второй — множитель и разделим обе части неравенства на -20, поменяв при этом его знак:
Видно, что выражение слева может быть меньше нуля только при (так как второй множитель всегда неотрицателен, ибо является полным квадратом), а равно нулю при или . Итак, окончательный ответ к данному неравенству:
.
Вот такое простое и изящное решение. При этом можете себе представить, что было бы, если бы мы решили воспользоваться стандартным методом решения неравенств с модулями и стали бы раскрывать модули при различных значениях .Рассмотрим ещё один пример решения неравенства с модулем методом рационализации. На этот раз из реального прототипа заданий для ЕГЭ по математике.
| Пример 4. Найдите все значения , при каждом из которых неравенствовыполняется при всех . |
Воспользуемся методом рационализации для решения данного неравенства с модулем. Заменим исходное неравенство равносильным ему неравенством без модулей:
После преобразования выражений, находящихся в скобках, получаем следующий результат:
Поскольку при всех значениях , то можно дважды умножить обе части полученного неравенства на , не меняя при этом знак неравенства. В результате приходим к следующему неравенству:
Или после умножения обеих частей на -1:
Последнее неравенство может быть выполнено для любых только в том случае, если обе соответствующие параболы, ветви которых направлены вверх, целиком лежат выше оси OX. Это условие выполняется в том случае, если дискриминанты обоих квадратных трёхчленов отрицательны. То есть имеет место система неравенств:
Решением этой системы является промежуток:
Примечание. Предвижу ваши возражения. Да, неравенство типа можно сразу заменить двойным неравенством . Здесь просто для иллюстрации предложен альтернативный способ решения неравенства методом рационализации.
На самом деле предложенный метод, конечно, работает не только с неравенствами, но и с уравнениями. Рассмотрим для примера решение следующего примера из реальных прототипов заданий ЕГЭ по математике.
| Пример 5. Найдите все значения , при каждом из которых уравнениеимеет более двух различных корней. |
Заменим данное уравнение следующим равносильным ему уравнением:
Или после упрощения выражений, стоящих в обеих скобках:
После вынесения общих множителей из скобок получаем:
Заметим, что при корень может быть любым числом. Этот случай нам подходит. Для разделим обе части этот уравнения на :
Данное уравнение может иметь от 1 до 3 корней. Нам нужны случаи, когда будет 3 различных корня. Один из этих корней обязательно будет равен .
Следовательно, задача сводится к поиску всех значений параметра , при каждом из которых квадратный трёхчлен, стоящий в скобках имеет два корня, каждый из которых отличен .
Это условие достигается тогда и только тогда, когда дискриминант этого квадратного трехчлена положителен и значение многочлена в скобках при не равно нулю. То есть имеет место система неравенств:Эту систему можно упростить:
Решением этой системы является промежуток:
.
Домашнее задание по решению неравенств методом рационализации
Итак, из этой статьи вы узнали, в чем состоит суть метода рационализации и научились применять его при решении логарифмических неравенств, а также неравенств, содержащих модули. Для того, чтобы закрепить полученные знания, предлагаю вам решить самостоятельно следующие неравенства:
(1)
(2)
Источник: https://yourtutor.info/%D0%BC%D0%B5%D1%82%D0%BE%D0%B4-%D1%80%D0%B0%D1%86%D0%B8%D0%BE%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7%D0%B0%D1%86%D0%B8%D0%B8-%D0%BD%D0%B5%D1%80%D0%B0%D0%B2%D0%B5%D0%BD%D1%81%D1%82%D0%B2
Метод рационализации. Часть 2
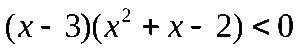
Метод рационализации позволяет перейти от неравенства, содержащего сложные показательные, логарифмические и т.п.выражения, к равносильному ему более простому рациональному неравенству.
Поэтому прежде чем мы начнем разговор про рационализацию в неравенствах, поговорим о равносильности. Если Вам тема знакома, и Вы просто хотите уточнить приемы рационализации, – вам сюда.
Равносильными или эквивалентными называются уравнения (неравенства), множества корней которых совпадают. Равносильными также считаются уравнения (неравенства), которые не имеют корней.
Пример 1. Уравнения и равносильны, так как имеют одни и те же корни.
Пример 2. Уравнения и также равносильны, так как решением каждого из них является пустое множество.
Пример 3. Неравенства и равносильны, так как решением и того, и другого является множество .
Пример 4. и – неравносильны. Решение второго уравнения является только 4, а решением первого – и 4, и 2.
Пример 5. неравенство равносильно неравенству , так как и в том, и в другом неравенствах – решение – это 6.
То есть по виду равносильные неравенства (уравнения) могут быть совсем далеки от сходства.
По сути, когда мы решаем сложные, длинные уравнения (неравенства), вроде этого , и получаем ответ , у нас ведь в руках оказывается ни что иное, как уравнение (неравенство), равносильное исходному. Вид разный, а суть одна!
Пример 6. Давайте вспомним, как мы решали неравенство до знакомства с методом интервалов. Мы заменяли исходное неравенство совокупностью двух систем:
То есть неравенство и последняя совокупность – равносильны между собой.
Также, мы могли бы, имея в руках совокупность
заменить ее неравенством , которое в два счета решается методом интервалов.
Мы вплотную подошли к методу рационализации в логарифмических неравенствах.
Метод рационализации в логарифмических неравенствах
Рассмотрим неравенство .
Представляем 4 в виде логарифма:
.
Мы имеем дело с переменным основанием у логарифма, поэтому, в зависимости от того, больше 1 или меньше 1 основание логарифма (то есть с возрастающей или убывающей функцией мы имеем дело), знак неравенства сохранится или поменяется на «». Поэтому возникает совокупность (объединение) двух систем:
Но, ВНИМАНИЕ, эта система должна решаться с учетом ОДЗ! Я специально не стала нагружать систему ОДЗ, чтобы не затерялась главная мысль.
Смотрите, вот мы сейчас перепишем нашу систему так (перенесем в каждой строке неравенства все в левую сторону):
Вам это ничто не напоминает? По аналогии с примером 6 мы данную совокупность систем заменим неравенством:.
Решив данное неравенство на ОДЗ мы и получим решение неравенства .
Найдем сначала ОДЗ исходного неравенства (ОДЗ для логарифмов смотрим здесь):
Теперь решим
Решение последнего неравенства с учетом ОДЗ:
Ответ: .
Итак, вот она, эта «волшебная» таблица:
Заметим, таблица работает при условии
где – функции от ,
– функция или число,
– один из знаков
Заметим также, вторая и третья строчки таблицы – следствия первой. Во второй строке 1 представлена прежде как , а в третьей – 0 представлен как .
И еще парочка полезных следствий (надеюсь, вам несложно понять откуда они вытекают):
где – функции от , – функция или число, – один из знаков
Метод рационализации в показательных неравенствах
Решим неравенство .
Решение исходного неравенства равносильно решению неравенства
.
Ответ: .
Таблица для рационализации в показательных неравенствах:
– функции от , – функция или число, – один из знаков Таблица работает при условии . Также в третьей, четвертой строках – дополнительно –
Опять же, по сути, нужно запомнить первую и третью строчки таблицы. Вторая строка -частный случай первой, а четвертая строка – частный случай третьей.
Метод рационализации в неравенствах, содержащих модуль
Работая с неравенствами типа , где функции от некоторой переменной, можем руководствоваться следующими равносильными переходами:
Решим неравенство
Перейдем к равносильному неравенству:
Ответ: .
Здесь предлагаюпосмотреть краткую сводку-таблицу к теме “Рационализация неравенств”.
А здесь предлагаю ещерассмотреть несколько примеров по теме “Рационализация неравенств”.
Источник: https://egemaximum.ru/metod-racionalizacii-chast-1/
Математика 11 класс Мендель Виктор Васильевич доцент кафедры математики ДВГГУ Метод рационализации при решении показательных и логарифмических неравенств ВВЕДЕНИЕ
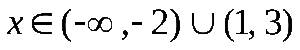
МИФ-2: Математика, информатика и физика – школьникам Хабаровского края
В предыдущей статье мы подробно рассмотрели методы решения рациональных и дробно-рациональных неравенств. В основе этих методов лежит очевидный факт: непрерывная функция на отрезке между двумя нулевыми значениями не изменяет знак (положительна или отрицательна).
Некоторые элементарные свойства многочленов, связанные с понятием кратного корня, позволяют быстро установить знак дробно-рациональной функции на каждом таком интервале монотонности.
Заметим, что в общем случае требуется вычислять значения функции в «пробных» точках на каждом интервале, что более трудоемко.
В этой статье мы рассмотрим примеры сведения логарифмических и показательных неравенств, у которых основание, выражение под знаком логарифма, степень – многочлены. Оказывается, такие неравенства эффективно сводятся к дробно-рациональным или рациональным, причем (что важно, например, на ЕГЭ) полученные решения будут более компактными по сравнению с традиционными.
Сведение логарифмического неравенства к системе рациональных неравенств
Рассмотрим логарифмическое неравенство вида
, (1)
где — некоторые функции (об их природе будем говорить ниже).
Стандартный метод решения такого неравенства предполагает разбор двух случаев на области допустимых значений неравенства.
В первом случае, когда основания логарифмов удовлетворяют условию
, знак неравенства обращается: .
Во втором случае, когда основание удовлетворяет условию , знак неравенства сохраняется: .
На первый взгляд – все логично, рассмотрим два случая и потом объединим ответы.
Правда, при рассмотрении второго случая возникает определенный дискомфорт – приходится на 90 процентов повторять выкладки из первого случая (преобразовывать, находить корни вспомогательных уравнений, определять промежутки монотонности знака). Возникает естественный вопрос – можно ли все это как-нибудь рационализировать объединить?
Ответ на этот вопрос содержится в следующей теореме.
Теорема 1.Логарифмическое неравенство
равносильно следующей системе неравенств:
(2)
Доказательство. Начнем с того, что первые четыре неравенства системы (2) задают множество допустимых значений исходного логарифмического неравенства. Обратим теперь внимание на пятое неравенство. Если , то первый множитель этого неравенства будет отрицателен.
При сокращении на него придется изменить знак неравенства на противоположный, тогда получится неравенство . Если же , то первый множитель пятого неравенства положителен, сокращаем его без изменения знака неравенства, получаем неравенство .
Таким образом, пятое неравенство системы включает в себя оба случая предыдущего метода. Терема доказана.
Пример. Решить неравенство
.
Решение. Воспользуемся теоремой 1. получим следующую систему неравенств:
Решая первые четыре неравенства, практически находим ОДЗ исходного неравенства:
Откуда: .
Решим теперь пятое неравенство системы. После элементарных преобразований получим неравенство
.
Умножим второй сомножитель на -1 и поменяем знак неравенства:
.
Нетрудно заметить, что корнями второго множителя в этом неравенстве являются числа 1 и -2. Поэтому, раскладывая второй множитель на одночлены первого порядка, получаем:
.
Это неравенство легко решить методом интервалов: .
С учетом найденного ранее ОДЗ, получаем окончательный ответ.
Ответ: .
Замечание. Обращаем внимание тех, кто собирается применять метод рационализации на ЕГЭ на следующее: критерии проверки таковы, что при ошибочном решении, но правильно найденном ОДЗ (при дополнительных условиях) можно получить балл. Поэтому рекомендуется сначала отдельно найти ОДЗ, а затем перейти к решению основного (пятого) неравенства.
Сведение показательного неравенства к системе рациональных неравенств
Теперь рассмотрим показательное неравенство вида
(3)
Так же, как в предыдущем пункте, — некоторые функции.
И снова вспомним, что традиционное решение такого неравенства приводит к двум случаям. В первом основание степени положительно, но меньше единицы (знак неравенства обращается), во втором случае основание степени больше единицы (знак неравенства сохраняется).
Как и в случае с логарифмическим неравенством, имеется возможность значительно укоротить решение задачи, используя метод рационализации. Этот метод основан на следующей теореме.
Теорема 2.Показательное неравенство
равносильно следующей системе неравенств:
(4)
Нетрудно заметить, что система (4) аналогична системе (2) из теоремы 1 (правда, в ней нет требования положительности степеней). Доказательство теоремы 2 легко получить теми же рассуждениями, что и в теореме 1.
Пример. Решить неравенство
.
Решение. Составим систему неравенств, аналогичную системе (4) из теоремы 2:
Решив два первых неравенства, найдем ОДЗ исходного показательного неравенства:
Откуда ОДЗ: .
Далее рассмотрим основное неравенство , которое упрощается к виду: .
Корни первого множителя этого неравенства мы нашли ранее: . Корни второго множителя равны: , , .Теперь перед нами встала нетривиальная задача упорядочения корней. Так как , то . Применив метод интервалов, получим следующее решение основного неравенства: .
Учитывая найденную ранее ОДЗ, получаем окончательный ответ:
.
Контрольная работа №2 для учащихся 11 классов
Приведенные ниже задания являются контрольной работой №2 для учащихся 11 классов. Каждая задача оценивается в 7 баллов, для зачета нужно набрать не менее 35 баллов.
Правила оформления работ:
Решения по каждому предмету оформляется отдельно. Каждое задание имеет свой шифр (М 11.2.1 и т.д.), который указывается перед записью решения.
Переписывать текст задачи не надо, достаточно краткой записи, если это необходимо. Оформлять решения в порядке следования заданий.
Можно присылать нам столько решений, сколько удалось вам сделать, даже если оказалось невозможным выполнить всю работу.
Наш адрес: 680000, г. Хабаровск, ул. Дзержинского, 48, ХКЦТТ (ХКЗФМШ).
Подробнее познакомиться со школой, ее традициями можно на нашем сайте: www.khspu.ru/~khpms/. Там же, на форуме, можно проконсультироваться по вопросам, связанным с решением задач (и не только).
Решите следующие неравенства
Источник: http://textarchive.ru/c-1925511.html

