Задачи на составление блок-схем алгоритмов
Алгоритмы. Разработка алгоритма решения задачи

Исключительно важно использовать язык блок-схем при разработке алгоритма решения задачи.
Решение одной и той же задачи может быть реализовано с помощью различных алгоритмов, отличающихся друг от друга как по времени счета и объему вычислений, так и по своей сложности.
Запись этих алгоритмов с помощью блок-схем позволяет сравнивать их, выбирать наилучший алгоритм, упрощать, находить и устранять ошибки.
Отказ от языка блок-схем при разработке алгоритма и разработка алгоритма сразу на языке программирования приводит к значительным потерям времени, к выбору неоптимального алгоритма. Поэтому необходимо изначально разработать алгоритм решения задачи на языке блок-схем, после чего алгоритм перевести на язык программирования.
При разработке алгоритма сложной задачи используется метод пошаговой детализации. На первом шаге продумывается общая структура алгоритма без детальной проработки отдельных его частей. Блоки, требующие детализации, обводятся пунктирной линией и на последующих шагах разработки алгоритма продумываются и детализируются.
В процессе разработки алгоритма решения задачи можно выделить следующие этапы:
- Этап 1 . Математическое описание решения задачи.
- Этап 2 . Определение входных и выходных данных.
- Этап 3 . Разработка алгоритма решения задачи.
Базовые алгоритмические конструкции
В теории программирования доказано, что для записи любого, сколь угодно сложного алгоритма достаточно трех базовых структур:
- следование (линейный алгоритм);
- ветвление (разветвляющийся алгоритм);
- цикл-пока (циклический алгоритм).
Линейные алгоритмы
Линейный алгоритм образуется из последовательности действий, следующих одно за другим. Например, для определения площади прямоугольника необходимо сначала задать длину первой стороны, затем задать длину второй стороны, а уже затем по формуле вычислить его площадь.
Пример
ЗАДАЧА. Разработать алгоритм вычисления гипотенузы прямоугольного треугольника по известным значениям длин его катетов a и b.
На примере данной задачи рассмотрим все три этапа разработки алгоритма решения задачи:
Этап 1. Математическое описание решения задачи.
Математическим решением задачи является известная формула:
,
где с-длина гипотенузы, a, b – длины катетов.
Этап 2. Определение входных и выходных данных.
Входными данными являются значения катетов a и b. Выходными данными является длина гипотенузы – c.
Этап 3. Разработка алгоритма решения задачи.
| Словесное описание алгоритма | Запись алгоритма на языке блок-схем |
|
На данной схеме цифрами указаны номера элементов алгоритма, которые соответствуют номерам пунктов словесного описания алгоритма. |
Разветвляющиеся алгоритмы
Алгоритм ветвления содержит условие, в зависимости от которого выполняется та или иная последовательность действий.
Циклические алгоритмы
Циклический алгоритм – определяет повторение некоторой части действий (операций), пока не будет нарушено условие, выполнение которого проверяется в начале цикла. Совокупность операций, выполняемых многократно, называется телом цикла.
Алгоритмы, отдельные действия в которых многократно повторяются, называются циклическими алгоритмами, Совокупность действий, связанную с повторениями, называют циклом.
При разработке алгоритма циклической структуры выделяют следующие понятия:
- параметр цикла – величина, с изменением значения которой связано многократное выполнение цикла;
- начальное и конечное значения параметров цикла;
- шаг цикла – значение, на которое изменяется параметр цикла при каждом повторении.
Цикл организован по определенным правилам. Циклический алгоритм состоит из подготовки цикла, тела цикла и условия продолжения цикла.
В подготовку цикла входят действия, связанные с заданием исходных значений для параметров цикла:
- начальные значения цикла;
- конечные значения цикла;
- шаг цикла.
В тело цикла входят:
- многократно повторяющиеся действия для вычисления искомых величин;
- подготовка следующего значения параметра цикла;
- подготовка других значений, необходимых для повторного выполнения действий в теле цикла.
В условии продолжения цикла определяется допустимость выполнения повторяющихся действий. Если параметр цикла равен или превысил конечное значение цикла, то выполнение цикла должно быть прекращено.
Пример
ЗАДАЧА. Разработать алгоритм вычисления суммы натуральных чисел от 1 до 100.
Этап 1. Математическое описание решения задачи.
Обозначим сумму натуральных чисел через S. Тогда формула вычисления суммы натуральных чисел от 1 до 100 может быть записана так:
где Xi – натуральное число X c номером i, который изменяется от 1 до n, n=100 – количество натуральных чисел.
Этап 2. Определение входных и выходных данных.
Входными данными являются натуральные числа: 1, 2, 3, 4, 5, …, 98, 99, 100.
Выходные данные – значение суммы членов последовательности натуральных чисел.
Параметр цикла – величина, определяющая количество повторений цикла. В нашем случае i – номер натурального числа.Подготовка цикла заключается в задании начального и конечного значений параметра цикла.
- начальное значение параметра цикла равно 1,
- конечное значение параметра цикла равно n,
- шаг цикла равен 1.
Для корректного суммирования необходимо предварительно задать начальное значение суммы, равное 0.
Тело цикла. В теле цикла будет выполняться накопление значения суммы чисел, а также вычисляться следующее значение параметра цикла по формулам:
S=S+i; I=I+1;
Условие продолжения цикла: цикл должен повторяться до тех пор, пока не будет добавлен последний член последовательности натуральных чисел, т.е. пока параметр цикла будет меньше или равен конечному значению параметра цикла.
Этап 3. Разработка алгоритма решения задачи.
Введем обозначения: S – сумма последовательности, i – значение натурального числа.
Начальное значение цикла i=1, конечное значение цикла i =100, шаг цикла 1.
| Словесное описание алгоритма | Запись алгоритма на языке блок-схем |
|
Источник: http://turbopro.ru/index.php/osnovy-programmirovaniya/6836-algoritmy-razrabotka-algoritma-resheniya-zadachi
Задачи на составление алгоритмов по информатике с решением | Помощь школьнику

Каталог заданий. Назад в каталог ? Вернуться к списку прототипов этой категории ? Версия для печати и копирования в MS Word. 1. Задание 6 № 47199. В треугольнике ABC , AD — высота, угол BAD равен Найдите угол C. Ответ дайте в градусах. Решение. Треугольник равнобедренный, значит, углы при.
Задачи на составление блок-схем алгоритмов
Задачи на составление блок-схем алгоритмов
Примеры определения результата выполнения алгоритма по заданной блок-схеме.
Пример 1. Дана блок-схема алгоритма
Определить результат выполнения алгоритма при определённых значениях исходных данных
Например, при x=16 и y=2
Дана блок-схема алгоритма
Определить результат выполнения алгоритма при определённых значениях исходных данных
Например, при x= — 6 или x=0 или x=7
Проверка условия x>0 «Нет» y= -2*(-6)=12
Проверка условия x>0 «Нет» y=-2*0=0 Вывод: y=0
Проверка условия x>0 «Да» y=2*7=14 Вывод: y=14
Дана блок-схема алгоритма
Определить результат выполнения алгоритма при определённых значениях исходных данных
Например, при n=15 или n=0 или n=-7
Проверка условия n>0 «Да»
Проверка условия n>0 «Нет» Проверка условия n0 «Нет» Проверка условия nC «Нет» B=9+8=17; F=7+17=24 Вывод F=24
2) Ввод: A=6; B=6; C=-10
Проверка условия A=B «Да» С=6+6=12; F=6+12=18 Вывод F=18
3) Ввод: A=6; B=10; C=-10
Проверка условия A=B «Нет» Ю Проверка условия B>C «Да» Ю A=6+10=16; F=16+(-10)=6 Вывод F=6
Дана блок-схема алгоритма
Например, при n=4 или n=1
Проверка условия k>2 «Да» S=0+4=4; n=4-1=3
Проверка условия k>2 «Да» S=4+3=7; n=3-1=2
Проверка условия k>2 «Нет» Вывод S=7
Проверка условия k>2 «Нет» Вывод S=0
Обзоры сервисов Pandia. ru
Товары
Мнение редакции может не совпадать с мнениями авторов.
Учебно-методический материал по информатике и икт (9 класс) на тему:
Решение задач на составление разветвляющихся алгоритмов
Цель: выработать умение решать задачи на составление алгоритмов на языке блок – схем.
+ Презентация и самостоятельная работа
Предварительный просмотр:
Тема: Решение задач на составление разветвляющихся алгоритмов.
Цели: выработать умение решать задачи на составление алгоритмов на языке
Оборудование: карточки с заданиями, мультимедийная презентация.
1. Актуализация знаний.
Диктант. Учащиеся выполняют диктант, Решение задач (одновременно с
Записывая ответы на листочках. диктантом). 2 ученика у доски.
1. Как обозначается блок означающий вычислительное действие (операцию присваивания)?
2. Как обозначается блок означающий ввод исходных данных, вывод результатов?
3. Разветвляющийся алгоритм – это алгоритм …
Ответ. … в котором в зависимости от истинности условия выполняется та или иная серия команд.
4. Как изображается в блок – схеме ветвление в полной форме?
5.Как оформляется в блок – схеме ветвление в неполной форме?
Теперь поменяйтесь листочками, проверьте, правильно ли ответили на вопрос ваш сосед и поставьте ему оценку (её определяет количество правильных ответов). (Ответы на слайдах).
Карточка №1. Функция y = f(х) задана графиком
Составьте блок-схему решения алгоритма.
2. Решение задач.
Определить результат выполнения алгоритма по его блок – схеме при заданных значениях а и в (а = 2, в = 3). Значения занести в таблицу.
(На примере задания карточки №2).
5 23 ? нет у = 10 + 3 = 13
25 23 ? да у = 25 + 2 2
Составить блок – схему алгоритма решения задачи. Переменной к присвоить номер четверти плоскости в которой находится точка с координатами х и у (х ≠ 0, у ≠ 0).
2. Найдите и исправьте ошибки в приведённой блок – схеме. Определите
Значения х и у в результате выполнения алгоритма по его блок – схеме при
Заданных значениях а, в. Значения переменных, изменяющиеся в процессе
Исполнения, занесите в таблицу.
1. Составьте по шаблону блок – схему решения задачи (шаблоны раздать
Заданы три числа – а, в, с. Известно, что два из них равны между собой, а третье отлично от них. Найдите, какое из чисел отлично от двух других.
Осуществить самопроверку (ответы на слайдах).
Ответы: I вариант
Приведите приведённую блок – схему в формульное описание (сведите все
Действия в одну формулу, если это возможно).
5. Итог урока. Кроссворд.
Ответы. По горизонтали: 1. Программа. 4. Результат. 7. Ветвление. 8. Схема.
По вертикали: 2. Алгоритм. 3. Аргумент. 5. Условие. 6. Бейсик.
6. Сообщение оценок.
7. Домашнее задание. Составить блок-схему алгоритма решения
Найдите и исправьте ошибки в приведённой блок – схеме. Определите значения х и у в результате выполнения алгоритма по его блок – схеме при заданных значениях а, в. Значения переменных, изменяющиеся в процессе исполнения, занесите в таблицу.
1. Составьте по шаблону блок – схему решения задачи.
Заданы три числа – а, в, с. Известно, что два из них равны между собой, а третье отлично
От них. Найдите, какое из чисел отлично от двух других.
2. Найдите и исправьте ошибки в приведённой блок – схеме. Определите значения х и у в
Результате выполнения алгоритма по его блок – схеме при заданных значениях а, в.
Значения переменных, изменяющиеся в процессе исполнения, занесите в таблицу.
По теме: методические разработки, презентации и конспекты
Основной этап урока – организация деятельности, направленная на применение полученных знаний и способов действий. Так же на уроке проводится работа по следующим направлениямработа с тестовы.
Цель урока: совершенствовать навыки составления пропорций по условию задачи, сформировать умение применять пропорции при решении задач, использовать условие и решение задачи для сохранения и укреплени.
Алгоритм решения задач на составление уравнений в 5 классе.
Тема урока: Базовый учебник АннотацияРешение задач на составление уравнений Учебно-методический комплект (УМК) «Математика» (авторы: Зубарева И. И., Мордкович А. Г. и др.
Презентация к уроку математики по теме: «Решение задач на составление уравнений».Данный материал пригодится как ученику, так и учителю. Разбор самых простых задач на составление линейных алгоритмов.
Алгоритмы с ветвящейся структурой

| Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 9 классы | Планирование уроков на учебный год | Оператор ветвления. Логические операции на Паскале
Уроки 32 — 33. Алгоритмы с ветвящейся структурой
Уроки 32 — 33. Сложные ветвящиеся алгоритмы
Уроки 32 — 33. Вопросы и задания
Уроки 32 — 33. Компьютерный практикум ЦОР. Алгоритмы с ветвящейся структурой (Задание 1 — 6)
Уроки 32 — 33. Компьютерный практикум ЦОР. Алгоритмы с ветвящейся структурой (Задание 7 — 12)
Уроки 32 — 33. Компьютерный практикум ЦОР. Алгоритмы с ветвящейся структурой (Задание 13 — 19)
Уроки 34 — 35. Программирование ветвлений на Паскале
Уроки 36 — 37. Программирование диалога с компьютером
Уроки 38 — 41. Разработка программы на языке Паскаль с использованием оператора ветвления и логических операций
Представление ветвлений на АЯ. Трассировка ветвящихся алгоритмов
Рассмотрим несколько задач, решение которых на компьютере получается с помощью ветвящихся алгоритмов.
Первая задача: даны два числа; выбрать большее из них.
Пусть исходными данными являются переменные А и B. Их значения будут задаваться вводом. Значение большего из них должно быть присвоено переменной С и выведено на экран компьютера. Например, если А = 5, В = 8, то должно получиться: С = 8.
Блок-схема алгоритма решения этой задачи изображена на рис. 2.2.
Нетрудно понять смысл этого алгоритма. Если значение переменной А больше, чем В, то переменной С присвоится значение А. В противном случае, когда А ≤ B, переменной С присвоится значение B.
Условием, по которому разветвляется алгоритм, является отношение неравенства А > B. Изучая базы данных и электронные таблицы, вы узнали, что такое отношение является логическим выражением.
Если оно справедливо, то результатом будет логическая величина «истина» и выполнение алгоритма продолжится по ветви «да»; в противном случае логическое выражение примет значение «ложь» и выполнение алгоритма пойдет по ветви «нет».
До выполнения на компьютере правильность алгоритма можно проверить путем заполнения трассировочной таблицы. Вот как будет выглядеть трассировка нашего алгоритма для исходных значений А = 5, В = 8.
Ветвление является структурной командой. Его исполнение происходит в несколько шагов: проверка условия (выполнения логического выражения) и выполнение команд на одной из ветвей «да» или «нет». Поэтому в трассировочной таблице записываются не команды алгоритма, а отдельные операции, выполняемые компьютером на каждом шаге.
В алгоритме на рис. 2.2 используется полное ветвление. Эту же самую задачу можно решить, применяя структурную команду неполного ветвления. Блок-схема такого алгоритма изображена на рис. 2.3.
Выполните самостоятельно трассировку этого алгоритма для вариантов 1) А = 0,2, В = 0,3; 2) А = 7, Б = 4; 3) А = 5, В = 5. Если вы всё проделаете правильно, то убедитесь, что алгоритм верный.
А теперь запишем рассмотренные алгоритмы на АЯ. Во-первых, нужно решить вопрос о том, как описать переменные в этом алгоритме. Для всех переменных в алгоритме на АЯ необходимо указать их тип.
Переменные А, В, С — числовые величины. В этой задаче они могут принимать любые значения. В программировании числовые величины, которые могут иметь любые значения — целые, дробные, называются вещественными. Им ставится в соответствие вещественный тип. На АЯ этот тип указывается служебным словом вещ.Как выглядит команда ветвления, вы уже знаете. Вот два алгоритма на АЯ, соответствующие блок-схемам на рис. 2.2 и 2.3.
Под сокращенным названием алгоритмов ВИД подразумевается «Большее из двух».
Для программирования характерно то, что одна и та же задача может быть решена с помощью разных алгоритмов. И чем сложнее задача, тем больше можно придумать различных алгоритмов ее решения. Для больших задач (производственных, научных) практически невозможно точное совпадение алгоритмов, составленных разными программистами.
Следующая задача: упорядочить значения двух переменных X и Y по возрастанию. Смысл этой задачи следующий: если для исходных значений переменных справедливо отношение X ≤ Y (например, X = 1, Y = 2), то оставить их без изменения; если же X > Y (например, X = 2, Y = 1), то выполнить обмен значениями.
Алгоритм обмена значениями двух переменных был рассмотрен в предыдущем параграфе. Вспомним, что для обмена мы использовали третью, вспомогательную переменную.
В алгоритме решения данной задачи используется неполное ветвление. Приведем блок-схему (рис. 2.4) и алгоритм на АЯ.
Здесь роль вспомогательной переменной для обмена выполняет С.
Источник: https://xn----7sbbfb7a7aej.xn--p1ai/informatika_09_sim/informatika_materialy_zanytii_09_32_41.html
Конспект урока на тему
Составление алгоритмов и блок-схем.
Цели урока:
Образовательные:
— формирование и закрепление навыков по составлению и выполнению алгоритмов;
— проверка знаний; — повышение интереса к изучению предмета;
— воспитание навыка быстрого мышления.
Развивающие:
— способствовать развитию умения планировать последовательность действий для достижения поставленной цели;
— способствовать развитию алгоритмического и логического мышления;
— развитие творческой активности учащихся;
— развитие познавательных интересов.
Воспитательная:
— способствовать воспитанию в детях ответственности, взаимопомощи и взаимоуважения
Тип урока: закрепление полученных знаний
Оборудование: Раздаточный материал, компьютер, проектор, презентация к уроку
Ход урока
-
Оргмомент. Взаимодействие учителя и учеников
-
Тема, цель. На прошлом уроке вы познакомились с важной темой информатики.
— Какой? ( Алгоритмы)
— Что такое алгоритм? (Порядок действий или план)
3. Устный опрос.
-Кто выполняет алгоритмы? (Исполнители)
Таблица 1. Определить соответствие в таблице.
|
Команда |
|
| Стиральная машина | Печатать |
| Собака | Полоскать |
| Человек | Сидеть |
| Компьютер | Сварить картофель |
— А каждый ли исполнитель может исполнить любую команду? Почему?
— Что такое система команд исполнителя?
— Какие команды выполняют эти исполнители?
Составить алгоритмы и блок-схемы к алгоритмам.
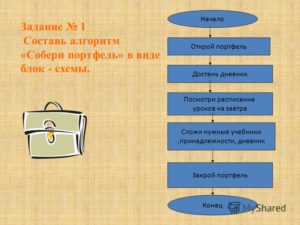
Задание 1.
Написать алгоритм сбора съедобных грибов, и составить к этому алгоритму блок-схему.
– Какая команда будет выполняться не всегда? Когда ее нужно пропустить? (команда «сорви гриб» не выполняется, если гриб несъедобный.) обвести прямоугольник с этой командой зеленым карандашом.
– Есть ли цикл в этом алгоритме? Какие команды будут выполняться больше одного раза? («найди гриб», «гриб съедобный», «сорви гриб», «все грибы обошел?».)
– Сколько раз будут выполняться эти 5 команд? («хитрость этого вопроса в том, что команды в цикле будут выполняться не одинаковое число раз: сорвать гриб нужно столько раз, сколько будет найдено съедобных грибов, а остальные 4 команды нужно выполнять столько раз, сколько будет найдено всех грибов.)
– В каком ромбе записано условие повтора?
(во втором ромбе, который нужно обвести красным карандашом.)
Задание 2.
Составить алгоритм разбора фасоли из мешка. Если фасоль белая, то её положить в круглую корзину, а если не белая, то в овальную корзину.
(Учесть, что задание допускает разное расположение команд на схеме).
Ответить на вопросы:
– Какие команды будут выполняться не всегда?
– Какие команды будут выполняться больше одного раза?
– Сколько раз будет выполнена каждая из этих команд?
– Какой вопрос на схеме является условием повтора?
Задание 3.
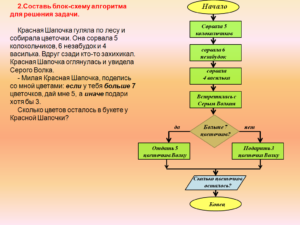
Составь блок-схему алгоритма для решения задачи.
Красная Шапочка гуляла по лесу и собирала цветочки. Она сорвала 5 колокольчиков, 6 незабудок и 4 василька. Вдруг сзади кто-то захихикал. Красная Шапочка оглянулась и увидела Серого Волка.
— Милая Красная Шапочка, поделись со мной цветами: если у тебя больше 7 цветочков, дай мне 5, а иначе подари, хотя бы 3.
Сколько цветов осталось в букете у Красной Шапочки?
-
Физкультминутка (3 мин)
-
Самостоятельная работа на компьютере по составлению алгоритмов и блок-схем. (15 мин)
8. Домашнее задание: составить текстовый и графические алгоритмы лепки снеговика.
Отлично поработали на уроке.
Получили «5»
Получили «4»
Чему вы сегодня научились?
Что вам сегодня понравилось?
– Закрепили знания о ветвлениях и циклах в алгоритмах.
– Научились отличать условие ветвления от условия повтора.
Сегодня вы научились составлять алгоритмы с ветвлениями и циклами.
Свежие документы: Конспект урока по Информатике «Антивирусы»
Источник: https://www.alllessons.ru/informatics/konspekt-uroka-na-temu-sostavlenie-algoritmov-i-blok-shem.html
«VBA Разработка алгоритма. Блок-схема. Структуры алгоритмов»
2.1 Разработка алгоритма.
2.2 Блок-схема.
2.3 Структуры алгоритмов.
2.1 Разработка алгоритма.
Алгоритм — это
a. описание последовательности действий для решения задачи или достижения поставленной цели;
b. правила выполнения основных операций обработки данных;
c. описание вычислений по математическим формулам.
Перед началом разработки алгоритма необходимо четко уяснить задачу: что требуется получить в качестве результата, какие исходные данные необходимы и какие имеются в наличии, какие существуют ограничения на эти данные. Далее требуется записать, какие действия необходимо предпринять для получения из исходных данных требуемого результата.
На практике наиболее распространены следующие формы представления алгоритмов:
словесная (записи на естественном языке); графическая (изображения из графических символов); псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.); программная (тексты на языках программирования).
Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задается в произвольном изложении на естественном языке.
Пример. Записать алгоритм нахождения наибольшего общего делителя (НОД) двух натуральных чисел.
Алгоритм может быть следующим:
1. задать два числа;
2. если числа равны, то взять любое из них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма;
3. определить большее из чисел;
4. заменить большее из чисел разностью большего и меньшего из чисел;
5. повторить алгоритм с шага 2.
Описанный алгоритм применим к любым натуральным числам и должен приводить к решению поставленной задачи. Убедитесь в этом самостоятельно, определив с помощью этого алгоритма наибольший общий делитель чисел 125 и 75.
Словесный способ не имеет широкого распространения по следующим причинам:
такие описания строго не формализуемы; страдают многословностью записей; допускают неоднозначность толкования отдельных предписаний. Графический способ представления алгоритмов является более компактным и наглядным по сравнению со словесным.
При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.
Такое графическое представление называется схемой алгоритма или блок-схемой.
Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов.
Он занимает промежуточное место между естественным и формальным языками.
С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи.
В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя.
Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда.
Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций.
2.2 Блок-схема
Блок-схемой называют графическое представление алгоритма, в котором он изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.
В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий.
Приведем наиболее часто употребляемые символы.
| Название символа | Обозначение и пример заполнения | Пояснение |
| Процесс | Вычислительное действие или последовательность действий | |
| Решение | Проверка условий | |
| Модификация | Начало цикла | |
| Предопределенный процесс | Вычисления по подпрограмме, стандартной подпрограмме | |
| Ввод-вывод | Ввод-вывод в общем виде | |
| Пуск-останов | Начало, конец алгоритма, вход и выход в подпрограмму | |
| Документ | Вывод результатов на печать |
Блок «процесс» применяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.
Блок «решение» используется для обозначения переходов управления по условию. В каждом блоке «решение» должны быть указаны вопрос, условие или сравнение, которые он определяет.
Блок «модификация» используется для организации циклических конструкций. (Слово модификация означает видоизменение, преобразование). Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.
Блок «предопределенный процесс» используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.Пример. Составить блок-схему алгоритма определения высот ha, hb, hc треугольника со сторонами a, b, c, если
где p = (a + b + c) / 2.
Решение. Введем обозначение тогда ha = t/a, hb = t/b, hc = t/c. Блок-схема должна содержать начало, ввод a, b, c, вычисление p, t, ha, hb, hc, вывод результатов и останов.
2.3 Структуры алгоритмов
Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых (т.е. основных) элементов. Естественно, что при таком подходе к алгоритмам изучение основных принципов их конструирования должно начинаться с изучения этих базовых элементов
Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: следование, ветвление, цикл.
Характерной особенностью базовых структур является наличие в них одного входа и одного выхода.
1. Базовая структура следование. Образуется из последовательности действий, следующих одно за другим:
2. Базовая структура ветвление. Обеспечивает в зависимости от результата проверки условия (да или нет) выбор одного из альтернативных путей работы алгоритма. Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран.
Структура ветвление существует в четырех основных вариантах:
если-то; если-то-иначе; выбор; выбор-иначе. 1) если-то если условие то действия конец если 2) если-то-иначе если условие то действия 1 иначе действия 2 конец если 3) выбор выбор при условие 1: действия 1 при условие 2: действия 2 . . . . . . . . . . . . при условие N: действия N конец выбора 4) выбор-иначе выбор при условие 1: действия 1 при условие 2: действия 2 . . . . . . . . . . . . при условие N: действия N иначе действия N+1 конец выбора
Пример. Составить блок-схему алгоритма вычисления функции
Базовая структура цикл. Обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла.
Структура цикл существует в трех основных вариантах:
Цикл типа для.
Предписывает выполнять тело цикла для всех значений некоторой переменной (параметра цикла) в заданном диапазоне.
Цикл типа пока.
Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное после слова пока.
Цикл типа делать — пока.
Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное после слова пока. Условие проверяется после выполнения тела цикла.
Заметим, что циклы для и пока называют также циклами с предпроверкой условия а циклы делать — пока — циклами с постпроверкой условия. Иными словами, тела циклов для и пока могут не выполниться ни разу, если условие окончания цикла изначально не верно. Тело цикла делать — пока выполнится как минимум один раз, даже если условие окончания цикла изначально не верно.цикл для i от i1 до i2 шаг i3 тело цикла (последовательность действий) конец цикла цикл пока условие тело цикла (последовательность действий) конец цикла цикл делать тело цикла (последовательность действий) пока условие конец цикла
Пример. Составить блок-схему алгоритма вычисления функции
yk = sin (kx) + cos (k/x), k = 1, 2, …, 50
Пример. Составить блок-схему вычисления функции
y = a3 / (a2 + x2)
при x, изменяющимся от x = 0 до x = 3 с шагом Dx = 0,1
Итерационные циклы. Особенностью итерационного цикла является то, что число повторений операторов тела цикла заранее неизвестно. Для его организации используется цикл типа пока. Выход из итерационного цикла осуществляется в случае выполнения заданного условия.
На каждом шаге вычислений происходит последовательное приближение и проверка условия достижения искомого результата.
Пример. Составить алгоритм вычисления суммы ряда
с заданной точностью (для данного знакочередующегося степенного ряда требуемая точность будет достигнута, когда очередное слагаемое станет по абсолютной величине меньше).
Вычисление сумм — типичная циклическая задача. Особенностью же нашей конкретной задачи является то, что число слагаемых (а, следовательно, и число повторений тела цикла) заранее неизвестно. Поэтому выполнение цикла должно завершиться в момент достижения требуемой точности.
При составлении алгоритма нужно учесть, что знаки слагаемых чередуются и степень числа х в числителях слагаемых возрастает.
Решая эту задачу «в лоб» путем вычисления на каждом i-ом шаге частичной суммы
S:=S+(-1)**(i-1)*x**i/i ,
мы получим очень неэффективный алгоритм, требующий выполнения большого числа операций. Гораздо лучше организовать вычисления следующим образом: если обозначить числитель какого-либо слагаемого буквой р, то у следующего слагаемого числитель будет равен -р*х (знак минус обеспечивает чередование знаков слагаемых), а само слагаемое m
будет равно p/i, где i — номер слагаемого.
Алгоритм, в состав которого входит итерационный цикл, называется итерационным алгоритмом. Итерационные алгоритмы используются при реализации итерационных численных методов.
В итерационных алгоритмах необходимо обеспечить обязательное достижение условия выхода из цикла (сходимость итерационного процесса). В противном случае произойдет зацикливание алгоритма, т.е.
не будет выполняться основное свойство алгоритма — результативность.
Вложенные циклы.Возможны случаи, когда внутри тела цикла необходимо повторять некоторую последовательность операторов, т. е. организовать внутренний цикл. Такая структура получила название цикла в цикле или вложенных циклов. Глубина вложения циклов (то есть количество вложенных друг в друга циклов) может быть различной.
При использовании такой структуры для экономии машинного времени необходимо выносить из внутреннего цикла во внешний все операторы, которые не зависят от параметра внутреннего цикла.
Пример вложенных циклов для. Вычислить сумму элементов заданной матрицы А(5,3).
Пример вложенных циклов пока. Вычислить произведение тех элементов заданной матрицы A(10,10), которые расположены на пересечении четных строк и четных столбцов.
Источник: http://www.mini-soft.ru/document/elektronnyy-uchebnik-po-vba-excel-2