Исследовательская работа по математике Кубическое уравнение и методы его решения
Самая удобная и увлекательная подготовка к ЕГЭ
![]()
Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, — правой частью уравнения.
Линейным называется такое уравнение, в котором неизвестное $x$ находится в числителе уравнения и без показателей. Например: $2х – 5 = 3$
Линейные уравнения сводятся к виду $ax = b$, которое получается при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей уравнения на число, отличное от нуля.
$5 (5 + 3х) — 10х = 8$
Раскроем скобки.
$25 + 15х — 10х = 8$
Перенесем неизвестные слагаемые в левую часть уравнения, а известные в правую. При переносе из одной части в другую, у слагаемого меняется знак на противоположный.
$15х — 10х = 8 — 25$
Приведем подобные слагаемые.
$5х = -17$ — это конечный результат преобразований.
После преобразований к виду $ax = b$, где, a=0, корень уравнения находим по формуле $х = {b}/{a}$
$х=-{17}/{5}$
$х = — 3,4$
Ответ: $- 3,4$
Квадратное уравнение — уравнение вида $ax2 + bx + c = 0$, где $a, b, c$ — некоторые числа a$≠0$, $x$ — неизвестное. Перед тем как решать уравнение, необходимо раскрыть скобки и собрать все слагаемые в левой части уравнения.
Числа $a, b, c$ называются коэффициентами квадратного уравнения.
- $a$ — старший коэффициент;
- $b$ — средний коэффициент;
- $c$ — свободный член.
Если в квадратном уравнении коэффициенты $b$ и $c$ не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение $2×2 – 8x + 3 = 0$. Если один из коэффициентов $b$ или $c$ равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным. Например, $5×2 – 2x = 0$.
Решение неполных квадратных уравнений
Неполное квадратное уравнение имеет вид $ax2 + bx = 0$, если $a$≠0$; $c$=0$. В левой части этого уравнения есть общий множитель $x$.
1. Вынесем общий множитель $x$ за скобки.
Мы получим $x (ax + b) = 0$. Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем $x = 0$ или $ax + b =0$. Таким образом, данное уравнение эквивалентно двум уравнениям:
$x = 0; ax + b = 0$
2. Решаем получившиеся уравнения каждое отдельно.
Мы получим $x = 0$ и $x={-b}/{a}$. Следовательно, данное квадратное уравнение имеет два корня $x = 0$ и $x={-b}/{a}$
$4х2 — 5х = 0$
Вынесем х как общий множитель за скобки:
$х (4х — 5) = 0$
Приравняем каждый множитель к нулю и найдем корни уравнения.
$x = 0$ или $4х — 5 = 0$
$х_1 = 0 х_2 = 1,25$
Ответ: $х_1 = 0; х_2 = 1,25$
Неполное квадратное уравнение вида $ax2 + c = 0, a≠0, b=0$
Для решения данного неполного квадратного уравнения выразим $x2$.
$ax2 + c = 0$
$ax2 = — c$
$x_2 = {-c}/{a}$
При решении последнего уравнения возможны два случая:
если ${-c}/{a}>0$, то получаем два корня: $x = ±v{{-c}/{a}}$
если ${-c}/{a} 0$. Тогда корни уравнения равны:
$x_{1,2}={-b±√D}/{2a}$
2. $D = 0$. В данном случае решение даёт два двукратных корня:
$x_{1}=x_{2}={-b}/{2a}$
3. $D < 0$. В этом случае уравнение не имеет корней.
$3х2 — 11 = -8х$
Соберем все слагаемые в левую часть уравнения и расставим в порядке убывания степеней$3х2 + 8х — 11 = 0$
$a = 3 ,b = 8, c = — 11$
$D = b2- 4ac = 82- 4 · 3 · (-11) = 196 = 142$
$x_{1}={-b+√D}/{2a}={-8+14}/{6}=1$
$x_{2}={-b-√D}/{2a}={-8-14}/{6}=-3{2}/{3}$
Ответ: $x_1=1, x_2=-3{2}/{3}$
Устные способы
Если сумма коэффициентов равна нулю $(а + b + c = 0)$, то $х_1= 1, х_2={с}/{а}$
$4х2+ 3х — 7 = 0$
$4 + 3 — 7 = 0$, следовательно $х_1= 1, х_2=-{7}/{4}$
Ответ: $х_1= 1, х_2 = -{7}/{4}$
Если старший коэффициент в сумме со свободным равен среднему коэффициенту $(a + c = b)$, то $х_1= — 1, х_2=-{с}/{а}$
$5х2+ 7х + 2 = 0$
$5 + 2 = 7$, следовательно, $х_1= -1, х_2 =-{2}/{5}$
Ответ: $х_1= -1, х_2 = -{2}/{5}$
Кубические уравнения
Для решения простых кубических уравнений необходимо обе части представить в виде основания в третьей степени. Далее извлечь кубический корень и получить простое линейное уравнение.
$(x — 3)3 = 27$
Представим обе части как основания в третьей степени
$(x — 3)3 = $33
Извлечем кубический корень из обеих частей
$х — 3 = 3$
Соберем известные слагаемые в правой части
$x = 6$
Ответ: $х = 6$
Дробно рациональные уравнения
Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.
Чтобы решить дробное уравнение, необходимо:
- найти общий знаменатель дробей, входящих в уравнение;
- умножить обе части уравнения на общий знаменатель;
- решить получившееся целое уравнение;
- исключить из его корней те, которые обращают в ноль общий знаменатель.
$4x + 1 — {3}/{x} = 0$
1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
2. находим общий знаменатель дробей и умножаем на него обе части уравнения
$4x + 1 — {3}/{x}= 0¦· x$
$4x · x + 1 · x — {3·x}/{x} = 0$
3. решаем полученное уравнение
$4×2 + x — 3 = 0$
Решим вторым устным способом, т.к. $а + с = b$
Тогда $х_1 = — 1, х_2 = {3}/{4}$
4. исключаем те корни, при которых общий знаменатель равен нулю В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $х_1 = — 1, х_2 = {3}/{4}$
При решении уравнения с двумя дробями можно использовать основное свойство пропорции.
Основное свойство пропорции: Если ${a}/{b} = {c}/{d}$, то $a · d = b · c$
${3х-5}/{-2}={1}/{х}$
Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
Воспользуемся основным свойством пропорции
$х (3х — 5) = -2$
Раскроем скобки и соберем все слагаемые в левой части уравнения
$3х2- 5х + 2 = 0$
Решим данное квадратное уравнение первым устным способом, т.к.
$a + b + c = 0$
$x_1 = 1, x_2 = {2}/{3}$
В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $x_1 = 1, x_2 = {2}/{3}$
Источник: https://examer.ru/ege_po_matematike/teoriya/kvadratnye_uravneniya
Научно-исследовательская работа «теорема виета для уравнений третьей и четвертой степени» математика
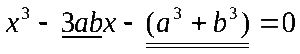
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа №64» г. Брянска
Городская научно-практическая конференция
«Первые шаги в науку»
Научно-исследовательская работа
«Теорема Виета для уравнений третьей и четвертой степени»
Математика
Выполнил: ученик 11б класса
Шанов Илья Алексеевич
Научный руководитель:
учитель математики,
кандидат физ.-мат. наук
Быков Сергей Валентинович
Брянск 2012
-
Введение ………………………………………………………………… 3
-
Цели и задачи …………………………………………………………… 4
-
Краткая историческая справка ………………………………………… 4
-
Квадратное уравнение …………………………………………………. 5
-
Кубическое уравнение …………………………………………………. 6
-
Уравнение четвертой степени ………………………………………… 7
-
Практическая часть ……………………………………………………. 9
-
Список литературы …………………………………………………… 12
-
Приложение …………………………………………………………… 13
Введение
Основная теорема алгебры утверждает, что поле является алгебраическим замкнутым, другими словами, что уравнения n-ой степени с комплексными коэффициентами (в общем случае) над полем имеет ровно n комплексных корней.
Уравнения третьей степени решаются формулой Кордано. Уравнения четвёртой степени методом Феррари. Кроме того, что в теории алгебры доказано, что если — корень уравнения, то так же является корнем этого уравнения.
Для кубического уравнения возможны следующие случаи:
-
все три корня – действительные;
-
два корня комплексных, один действительный.
Отсюда следует, что любое кубическое уравнение имеет хотя бы один действительный корень.
Для уравнения четвертой степени:
-
Все четыре корня различные.
-
Два корня действительных, два – комплексных.
-
Все четыре корня комплексные.
Данная работа посвящена тщательному изучению теоремы Виета: её формулировке, доказательству, а так же решению задач с применением этой теоремы.
Проделанная работа направлена помощь ученика 11-х классов, которым предстоит сдача ЕГЭ, а так же для юных математиков, которым небезразличны более простые и эффективные методы решений в различных областях математики.
В приложении к этой работе предоставляется сборник задач для самостоятельного решения и закрепления нового материала, исследуемого мной.
Этот вопрос нельзя оставлять без внимания, так как он важен для математики как для науки в целом, так и для учащихся и интересующихся решение подобных задач.
Цели и задачи работы:
- Получить аналог теоремы Виета для уравнения третьей степени.
- Доказать аналог теоремы Виета для уравнения третьей степени.
- Получить аналог теоремы Виета для уравнения четвертой степени.
- Доказать аналог теоремы Виета для уравнения четвертой степени.
- Рассмотреть применения данных вопросов к решению практических задач.
- Убедиться в практичности применения данной теоремы.
- Углубить математические знания в области решения уравнений.
- Развить интерес к математике.
Краткая историческая справка
О свойствах корней ТЕОРЕМА ВИЕТА…
ФРАНСУА ВИЕТ(1540—1603) — французский математик. По профессии юрист. В 1591 году ввёл буквенные обозначения не только для неизвестных величин, но и для коэффициентов уравнений; благодаря этому стало впервые возможным выражение свойств уравнений и их корней общими формулами.
Ему принадлежит установление единообразного приёма решения уравнений 2-й, 3-й и 4-й степеней. Среди открытий сам Виет особенно высоко ценил установление зависимости между корнями и коэффициентами уравнений.
Для приближённого решения уравнений с численными коэффициентами Виет предложил метод, схожий с позднейшим методом Ньютона.
В тригонометрии Франсуа Виет дал полное решение задачи об определении всех элементов плоского или сферического треугольника по трём данным, нашёл важные разложения cos nх и sin nх по степеням cos х и sin х. Он впервые рассмотрел бесконечные произведения. Сочинения Виета написаны трудным языком и поэтому получили в свое время меньшее распространение, чем заслуживали.Квадратное уравнение
Для начала вспомним формулы Виета для уравнения второй степени, которые мы узнали в программе школьного курса обучения.
Теорема Виетадля квадратного уравнения (8 класс)
Если и – корни квадратного уравнения то
т. е. сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Так же, вспомним теорему, обратную теореме Виета:
Если числа —p и q таковы, что
то и — корни уравнения
Теорема Виета замечательна тем, что, не зная корней квадратного трехчлена, мы легко можем вычислить их сумму и произведение, то есть простейшие симметричные выражения.
Теорема Виета позволяет угадывать целые корни квадратного трехчлена.
Кубическое уравнение
Теперь перейдём, непосредственно, к постановке и решению кубического уравнения с помощью теоремы Виета.
Формулировка
Кубическое уравнение — это уравнение третьего порядка, вида
где a ≠ 0.
Если а = 1, то уравнение называют приведённым кубическим уравнением:
Итак, нужно доказать, что для уравнения
справедлива следующая теорема:
пусть корни данного уравнения, тогда
Доказательство
Представим многочлен
в виде
выполним преобразования:
Итак, получим, что
Два многочлена равны тогда и только тогда, когда равны их коэффициенты при соответствующих степенях.
Это значит, что
https://www.youtube.com/watch?v=5P9ptyUnkzo
Что и требовалось доказать.
Теперь рассмотрим теорему, обратную теореме Виета для уравнения третьей степени.
Формулировка
Если числа таковы, что
то эти числа являются корнями уравнения
Уравнение четвертой степени
Теперь перейдём к постановке и решению уравнения четвертой степени с помощью теоремы Виета для уравнения четвертой степени.
Формулировка
Уравнение четвертой степени — уравнение вида
где a ≠ 0.
Если а = 1, то уравнение называют приведённым
Итак, докажем, что для уравнения
справедлива следующая теорема: пусть корни данного уравнения, тогда
Доказательство
Представим многочлен
в виде
выполним преобразования:
Итак, получим, что
Мы знаем, что два многочлена равны тогда и только тогда, когда равны их коэффициенты при соответствующих степенях.
Это значит, что
https://www.youtube.com/watch?v=5P9ptyUnkzo
Что и требовалось доказать.
Рассмотрим теорему, обратную теореме Виета для уравнения четвёртой степени.
Формулировка
Если числа таковы, что
то эти числа являются корнями уравнения
Практическая часть
Теперь рассмотрим решения задач, с помощью теорем Виета для уравнений третьей и четвертой степени.
Задача №1
-
Найти сумму и произведение корней уравнения
-
Решение: воспользуемся теоремой Виета, тогда получим, что
Ответ: 4, -4.
Задача №2
-
Найти сумму и произведение корней уравнения
-
Решение: воспользуемся теоремой Виета, тогда получим, что
Ответ: 16, 24.
Для решения данных уравнений можно использовать формулы Кардано и метод Феррари соответственно, но, используя теорему Виета, мы заведомо знаем сумму и произведение корней этих уравнений.
Задача №3
-
Составить уравнение третьей степени, если известно, что сумма корней равна 6, по парное произведение корней равно 3, а произведение -4.
-
Решение: пользуясь формулой Виета, получим
Составим уравнение, получим
Ответ:
Задача №4
-
Составить уравнение третьей степени, если известно, что сумма корней равна 8, по парное произведение корней равно 4, утроенные произведение равно 12, а произведение 20.
-
Решение: пользуясь формулой Виета, получим
Составим уравнение, получим
Ответ:
С помощью теоремы Виета мы легко составили уравнения по их корням. Это самый рациональный способ решения данных задач.
Задача №5
-
Найдите S треугольника, длины сторон которого есть корни уравнения
-
Решение: воспользуемся формула Герона
где a, b, c – формулы Герона.
Раскроем скобки и преобразуем выражение, получим
Заметим, что подкоренное выражение является кубическим выражением. Воспользуемся теоремой Виета для соответствующего ему кубического уравнения, тогда имеем, что
Зная, что получим:
Ответ:
Из решения этой задачи видно, что теорема Виета применима к задачам из разных областей математики.
Заключение
В данной работе был исследован метод решения уравнения третьей и четвертой степеней с помощью теоремы Виета. Выведенные в работе формулы просты в использовании. В ходе исследования стало очевидно, что в некоторых случаях этот метод эффективен больше, чем формула Кордано и метод Феррари для уравнений третьей и четвёртой степеней соответственно.
Теорема Виета была применена на практике. Был решён ряд задач, которые помогли лучше закрепить новый материал.
Это исследование было для меня очень интересным и познавательным. Углубив свои знания в математике, я открыл много интересного и с удовольствием занимался данным исследованием.Но мое исследование в области решения уравнений на этом не закончено. В будущем я планирую заняться исследованием решения уравнения n-ой степени с помощью теоремы Виета.
Хочу выразить огромную благодарность своему научному руководителю, кандидату физико-математических наук, а возможность такого необычного исследования и постоянное внимание в работе.
Список литературы
-
Виноградов И.М. Математическая энциклопедия. М., 1977.
-
В. Б. Лидский, Л. В. Овсянников, А. Н. Тулайков, М. И. Шабунин. Задачи по элементарной математике, Физматлит, 1980.
Приложение 1. (Презентация)
Для воспроизведения презентации нужно дважды щелкнуть на область картинки (воспроизводится через PowerPoint)).
Источник: http://textarchive.ru/c-1801642.html
Решение кубических уравнений. Формула Кардано
![]()
| Справочник по математике | Алгебра | Кубические уравнения |
Целью данного раздела является вывод формулы Кардано для решения уравнений третьей степени (кубических уравнений)
| a0x3 + a1x2 + + a2x + a3= 0, |
(1) |
где a0, a1, a2, a3 – произвольные вещественные числа,
Вывод формулы Кардано состоит из двух этапов.
На первом этапе кубические уравнения вида (1) приводятся к кубическим уравнениям, у которых отсутствует член со второй степенью неизвестного. Такие кубические уравнения называют трёхчленными кубическими уравнениями.
На втором этапе трёхчленные кубические уравнения решаются при помощи сведения их к квадратным уравнениям.
Приведение кубических уравнений к трехчленному виду
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
| x3 + ax2 + bx + c = 0, | (2) |
где a, b, c – произвольные вещественные числа.
Заменим в уравнении (2) переменную x на новую переменную y по формуле:
| (3) |
Тогда, поскольку
то уравнение (2) примет вид
В результате уравнение (2) примет вид
| (4) |
Если ввести обозначения
то уравнение (4) примет вид
где p, q – вещественные числа.
Уравнения вида (5) и являются трёхчленными кубическими уравнениями, у которых отсутствует член со второй степенью неизвестного.
Первый этап вывода формулы Кардано завершён.
Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи
Следуя методу, примененому Никколо Тартальей (1499-1557) для решения трехчленных кубических уравнений, будем искать решение уравнения (5) в виде
| (6) |
где t – новая переменная.
Поскольку
то выполнено равенство:
Следовательно, уравнение (5) переписывается в виде
| (7) |
Если теперь уравнение (7) умножить на t, то мы получим квадратное уравнение относительно t :
| (8) |
Формула Кардано
Решение уравнения (8) имеет вид:
В соответствии с (6), отсюда вытекает, что уравнение (5) имеет два решения:
| (9) |
В развернутой форме эти решения записываются так:
| (10) |
| (11) |
Покажем, что, несмотря на кажущиеся различия, решения (10) и (11) совпадают.
Действительно,
С другой стороны,
Таким образом,
и для решения уравнения (5) мы получили формулу
| (12) |
которая и называется «Формула Кардано».
Замечание. Поскольку у каждого комплексного числа, отличного от нуля, существуют три различных кубических корня, то, для того, чтобы избежать ошибок при решении кубических уравнений в области комплексных чисел, рекомендуется использовать формулу Кардано в виде (10) или (11).
Пример решения кубического уравнения
Пример. Решить уравнение
| x3 – 6×2 – 6x – 2 = 0. | (13) |
Решение. Сначала приведем уравнение (13) к трехчленному виду. Для этого в соответствии с формулой (3) сделаем в уравнении (13) замену
Тогда получим
x3 – 6×2 – 6x – 2 =
= (y + 2)3– 6(y + 2)2 –
– 6(y + 2) – 2 =
= y3 + 6y2 + 12y + 8 – 6y2 –
– 24y – 24 – 6y – 12 – 2 =
= y3 – 18y – 30.
Следовательно, уравнение (13) принимает вид
Теперь в соответствии с формулой (6) сделаем в уравнении (15) еще одну замену
| (16) |
Тогда поскольку
то уравнение (15) примет вид
| (17) |
Далее из (17) получаем:
Отсюда по формуле (16) получаем:
| (18) |
Заметим, что такое же, как и в формуле (18), значение получилось бы, если бы мы использовали формулу
или использовали формулу
Далее из равенства (18) в соответствии с (14) получаем:
Таким образом, мы нашли у уравнения (13) вещественный корень
Замечание 1. У уравнения (13) других вещественных корней нет.
Замечание 2. Поскольку произвольное кубическое уравнение в комплексной области имеет 3 корня с учетом кратностей, то до полного решения уравнения (13) остается найти еще 2 корня.
Эти корни можно найти разными способами, в частности, применив вариант формулы Кардано для области комплексных чисел.
Однако применение такого варианта формулы Кардано значительно выходит за рамки курса математики даже специализированных математических школ.
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
|
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
| подготовительные курсы для школьников 8, 9, 10 и 11 классов |
У нас также для школьников организованы
| индивидуальные занятия с репетиторами по математике и русскому языку |
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
Источник: https://www.resolventa.ru/spr/algebra/cardano.htm

